 |
Kürzel und Tipps zu wolframalpha.com; wie ging noch der Befehl fürs Integrieren, Ableiten, anderes? |
Kürzel und Tipps zu WolframAlpha
Kürzel und Tipps zu wolframalpha.com; wie ging noch der Befehl fürs Integriern, Ableiten, anderes?
Quelle: http://www.ruhr-uni-bochum.de/mathe-wiwi/skripte/Wolfram%20Alpha.pdf- Ableiten
 sin(x^3+x+1)‘
d/dy(d/dx sin(xy))
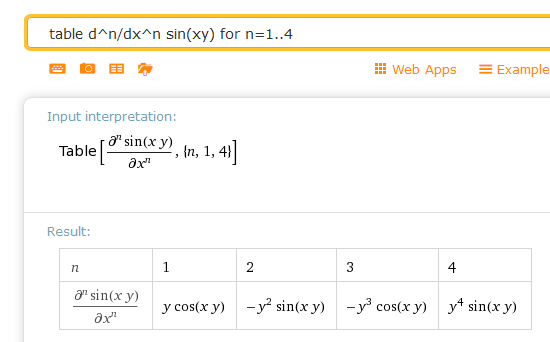
table d^n/dx^n sin(xy) for n=1..4
sin(x^3+x+1)‘
d/dy(d/dx sin(xy))
table d^n/dx^n sin(xy) for n=1..4
- Integrieren integral xe^x integral(0,1) xe^x integral(1,8) 2/(yx^(1/3)) dx definite integral integral –x^2-y^2+4 dy dx over 0<=y<=1,0<=x<=2
- vereinfachen simplify 2x^2-7xy+3y^2 factor 2x^2-7xy+3y^2 factor 7654 cancel ((x^3-1)/(x-1)) apart (x^2+3x+4)/(x(x+1))
- Gleichungen, Ungleichungen solve x^2-3x+2=0 Nullstellen roots x^2-3x+2 solve 2x+3y=8,3x+4y=11 solve 18<100/(19-x)+x<20 for integer x (Differenzialgleichung) solve x‘‘(t)-2x‘(t)+3x(t)=t+1,x(0)=1,x‘(0)=1
- Grenzwerte lim (x^n-1)/(x-1),x to 1 lim (x^n-1)/(x-1),x->1 lim (1+1/n)^n,n to infy
- Summe, Produkt sum k^2,k,1,n sum k^-2,k,1,infy product (k+2)/(k+1),k,0,n
- Taylorreihe: series e^x/sin(x),x=0
- Maximum, Minimum: max -x^3+3x+1 on -2<=x<=2
- Lineare Optimierung: max x+y on x<=12,y<=10,x+2y<=26,2x+y<=28
- Länge eines Vektors: norm{1,2,2}
- Matrixmultiplikation: {{1,2,3},{0,a,1}}.{{2},{1},{3}} {{1,2,3},{0,a,1}}.{{2,1},{b,3},{1,0}}
- Determinante: det{{12},{3,4}}
- Inverse: inverse{{1,2,3},{3,4,5},{a,0,0}}
- Eigenwerte: eigenvalue{{1,2,2},{2,2,1},{2,1,2}}

